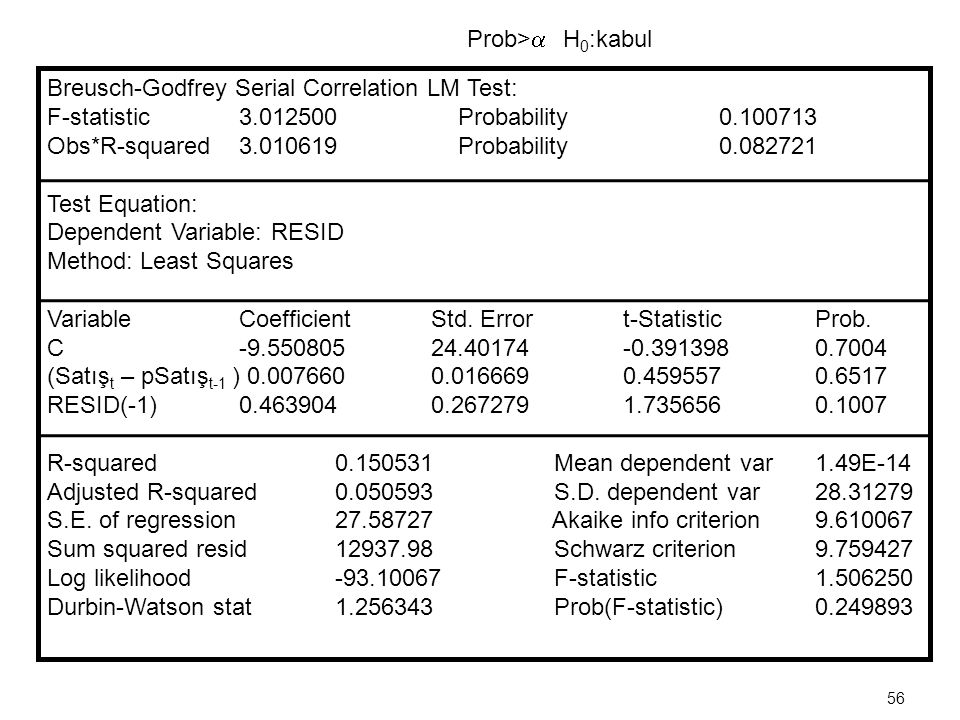

Kaspersky Internet Security 7.0.1.321 Final With Valid Key. Breusch-Godfrey LM test for serial correlation Consider: Y = Xβ+u in which we suspect that utis first order serially corre-lated, i.e. Ut= ρ1ut−1 +εt. The Breusch–Godfrey serial correlation LM test is a test for autocorrelation in the errors in a regression model. It makes use of the residuals from the.
In, the Breusch–Godfrey test, named after and, is used to assess the validity of some of the modelling assumptions inherent in applying models to observed data series. In particular, it for the presence of that has not been included in a proposed model structure and which, if present, would mean that incorrect conclusions would be drawn from other tests, or that sub-optimal estimates of model parameters are obtained if it is not taken into account.
The regression models to which the test can be applied include cases where lagged values of the are used as in the model's representation for later observations. This type of structure is common in. A similar assessment can be also carried out with the. Because the test is based on the idea of, it is sometimes referred to as LM test for serial correlation. Contents • • • • • • Background The Breusch–Godfrey serial correlation LM test is a test for in the in a regression model.
It makes use of the from the model being considered in a, and a test statistic is derived from these. The is that there is no of any order up to p. The test is more general than the (or Durbin's h statistic), which is only valid for nonstochastic regressors and for testing the possibility of a first-order autoregressive model (e.g. AR(1)) for the regression errors. [ ] The BG test has none of these restrictions, and is statistically more than Durbin's h statistic.
[ ] Procedure Consider a of any form, for example where the residuals might follow an AR( p) autoregressive scheme, as follows: The simple regression model is first fitted by to obtain a set of sample residuals. Beckman Coulter Software there. Breusch and Godfrey [ ] proved that, if the following auxiliary regression model is fitted and if the usual statistic is calculated for this model, then the following can be used for the distribution of the test statistic when the null hypothesis holds (that is, there is no serial correlation of any order up to p). Here n is the number of data-points available for the second regression, that for, where T is the number of observations in the basic series. Note that the value of n depends on the number of lags of the error term ( p). Software • In, this test is performed by function bgtest, available in lmtest. • In, this test is performed by the command estat bgodfrey.